
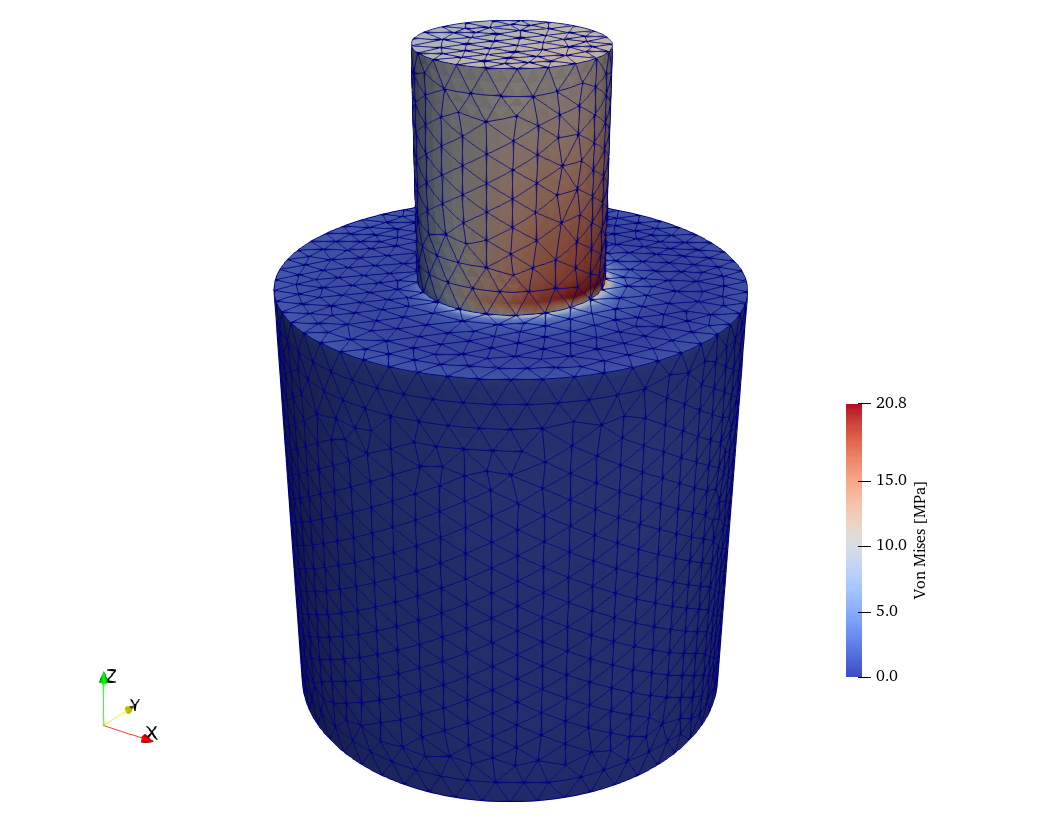
Where Γ is the strength of the vortex circulation. The superimposed stream function and velocity potential now consist of When the solutions obtained previously for flow past a fixed cylinderĪre combined with a vortex, flow past a rotating cylinder can be simulated. This discrepancy is referred to as d'Alembert's To separate away from the cylinder, and the drag is nonzero However, as will be discussed in the Lift section, when a real fluid flows past a cylinder, viscous effectsĪre important near the cylinder. Section are based on the assumption of inviscid flow (i.e., zero viscosity), The potential flow solutions developed in this When the integrations are carried out for F x and F y (integration details are not given for simplicity), it is found that both drag and lift are zero for potential flow. Lift is the resultant force acting perpendicular to the uniform flow Its direction is parallel to the upstream uniform flow direction. The drag developed on the cylinderĬan be obtained by integrating the pressureĭrag is the resultant force exerted by the fluid on the cylinder, and The concepts of drag and lift will be briefly introduced here. The discrepancy between theĮxperimental and theoretical results, as shown in the figure, is due to Where C p is the dimensionless pressure coefficient. Substituting the expression for v θs into The elevationĬhanges are assumed negligible. "s" refers to the condition along the cylinder. Where the subscript "o" refers to the upstream condition while The cylinder can be obtained using Bernoulli's equation, To a maximum velocity of 2U at the top and bottom of the cylinder (θ = π/2 The radial velocity component is always zero along the cylinder while Velocity components can be determined by:Īlong the cylinder (r = a), the velocity components reduce to The plot of the streamlines is shown in the figure. The stream function and velocity potential for flow past a fixed circular Which gives the strength of the doublet as Has a value of zero, the stream function on the surface of the cylinder Since the streamline that passes through the stagnation point The superimposed stream function and velocity potential are given by In this section, the solutions for potential flow past a fixed and rotating circular cylinder will be obtained by the method of superposition.įlow past a fixed circular cylinder can be obtained by combiningĭoublet. Solver.Fluids eBook: Flow around a Circular Cylinder Solver = NonlinearVariationalSolver(problem) Problem = NonlinearVariationalProblem(F, w, bcs, J) # combine variational forms with time derivative # variational form without time derivative in current timeį1_eq1 = (inner(T, grad(u)) + inner(grad(v)*v, u))*dx # Define variational forms without time derivative in previous timeį0_eq1 = (inner(T0, grad(u)))*dx + inner(grad(v0)*v0, u)*dx
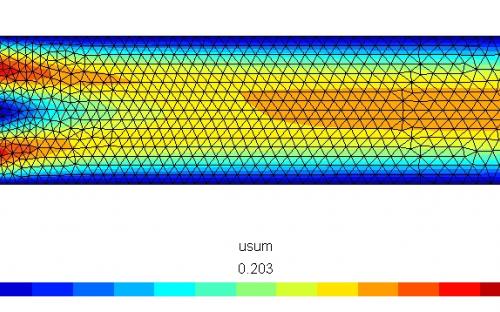
I = Identity(V.cell().d) # Identity tensor # Inflow boundary condition for velocity and temperature # No-slip boundary condition for velocityīc0 = DirichletBC(W.sub(0), noslip, Walls()) Return (on_boundary and (x (2.2 - DOLFIN_EPS)))īoundary_parts = MeshFunction("size_t", mesh, mesh.topology().dim()-1) Return(on_boundary and (r (0.41 - DOLFIN_EPS)))) But I suspect that mesh size h computed as 2*circumradius is not good quantity and prefer cell diameter computed this way from dolfin import * You can also uncomment SUPG/PSPG stabilization. This is I think rotating cylinder and Karman vortex street behind it.


 0 kommentar(er)
0 kommentar(er)
